Gesamtsteifigkeitsmatrix
Aus ESOCAETWIKIPLUS
engl: system stiffness matrix Kategorie: ![]() Level 1 Theorie
Level 1 Theorie
Die Gesamtsteifigkeitsmatrix ist die Steifigkeitsmatrix des gesamten Berechnungsmodells.
Der Begriff der Steifigkeitsmatrix ist üblich für die Matrix der
Zahlenwerte, die mit den Freiheitsgraden im Gleichungssystem verknüpft sind.
Der Begriff ist direkt verständlich bei Anwendungen der Strukturmechanik, bei denen diese Zahlenwerte die Steifigkeiten im Bauteil repräsentieren. Der Begriff Gesamtsteifigkeitsmatrix ist durchaus auch üblich für solche Anwendungen, bei denen andere physikalische Größen repräsentiert werden wie zum Beispiel Temperaturfelder oder Magnetfelder.
Die Gesamtsteifigkeitsmatrix wird bei der Lösung einer FEM-Aufgabenstellung verwendet, um die unbekannten Freiheitsgrade zu berechnen.
Beachten Sie, dass bei der Lösung einer FEM-Berechnung das Steifigkeitsverhältnis der Zahlenwerte auf der Hauptdiagonalen einen Einfluss auf den Rundungsfehler hat.
Beispiel
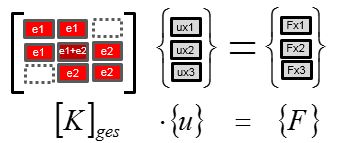
In dem Beispiel zum Selbststudium "FEM Handrechnung" ist dargestellt, wie die Koeffizienten der Elementsteifigkeitsmatrizen bestimmte Plätze im Gleichungssystem (der Gesamtsteifigkeitsmatrix) einnehmen. Es ist ein Beispiel mit zwei Stab-Elementen. Jedes der Elemente hat zwei Knoten mit jeweils einem Freiheitsgrad.
Grafisch dargestellt ist die Elementsteifigkeitsmatrix Ke jedes Elementes (so wie hier zusammen mit den Verschiebungen u und den Kräften F an den zugehörigen Knoten dargestellt)
im Gleichungssystem in der Gesamtsteifigkeitsmatrix Kges links wiederzufinden
Es ist zu erkennen, wie die Zahlenwerte jedes Elements in die Gesamtsteifigkeitsmatrix eingebracht werden und wo sie dort einen Beitrag liefern (nämlich in den Zeilen und Spalten, die zu den jeweiligen Freiheitsgraden der Eckknoten gehören).
Im technischen Alltag enthält die Gesamtsteifigkeitsmatrix durchaus 1 Mio x 1 Mio Zahlenwerte, weil Modelle mit 1 Mio Freiheitsgrade durchaus üblich und schnell lösbar sind.
Einige typische Eigenschaften der Gesamtsteifigkeitsmatrix sind:
- die Zahlenwerte auf der Hauptdiagonalen dürfen nicht kleiner oder gleich Null sein (sie muss positiv definit sein) und
- sie ist meistens schwach besetzt (es gibt also viele Positionen außerhalb der Hauptdiagonalen, die Null sind).
Selbststudium
Die Herleitung und Anwendung der Gesamtsteifigkeitsmatrix wird im Selbststudium-Beispiel des konischen Zugstabes im Detail erläutert.
Die Verwendung von verschiedenen Koordinatensystemen bei der Erstellung der Elementsteifigkeitsmatrix und der Gesamtsteifigkeitsmatrix beschreibt eine Folge "Steifigkeitsmatrizen und Koordinatensysteme" an einem Beispiel.