Effizienz

Aus ESOCAETWIKIPLUS

engl: simulation efficiency          Kategorie: Level 2 Theorie

Jeder, der eine Simulation durchführt, ist an einer möglichst hohen Effizienz der Simulation interessiert. Dabei wird als Effizienz das Verhältnis von Nutzen zu Aufwand angesehen, so dass das Ziel also

• ein möglichst hoher Nutzen (hohe Genauigkeit, schnelles Vorliegen des Ergebnisses) und
• ein möglichst geringer Aufwand (geringe Bearbeitungszeit, geringe Rechenzeit, geringe Softwarekosten).

Inhaltsverzeichnis 1 Simulation 2 Methoden 3 Anmerkungen 4 Fallbeispiele 5 Weiterführende Informationen

Simulation

Hier sind viele Methoden des high performance computing (HPC) aufgelistet, mit denen die Effizienz der Simulation beeinflusst werden kann. Diese Methoden betreffen teilweise

• die Idealisierung, Physik (Multiphysik): der Anwender trifft bereits bei der Idealisierung die Entscheidung über die Methode,
• Modellierung, Modellbildung, Diskretisierung: der Anwender trifft bei der Diskretisierung die Entscheidung,
• Lösung: Algorithmen, Steuerung, Zeitschritte: bei der Anwendung werden Steuerungen des Lösungsablaufes vorgenommen,
• Hardware: Hardware-Möglichkeiten werden vorausgesetzt und genutzt,
• Middleware: Hardware-nahe Software - z.B. Compiler - gehören zu der Methode.

Methoden

• Systemsimulation (Idealisierung): Kopplung von Simulations-Teilbereichen (Systemreduktion) und gemeinsame Lösung.

• Starke Kopplung (Physik (Multiphysik)): ein Modell wird für mehrere Physiken erstellt, die Kopplung bei der Multiphysik-Lösung erfolgt innerhalb der Matrizen, typische Anwendung: FEM bei Piezoelektrizität (Kopplung von elektrischem Feld und Strukturmechanik).

• Schwache Kopplung (Physik (Multiphysik)): ein Modell wird für mehrere Physiken erstellt, die Kopplung bei der Multiphysik-Lösung erfolgt über die Lastvektoren (rechte Seite des Gesamt-Gleichungssystems), typische Anwendung: Magnetfeld-Temperaturfeld oder Temperaturfeld-Strukturmechanik.

• sequentielle Kopplung (Physik (Multiphysik)): ein Modell wird für mehrere Physiken erstellt, uni-direktionale Kopplung von Physiken (also Lösung einer Physik und anschließend Lösung der nächsten Physik), typische Anwendung: transientes Temperaturfeld-Strukturmechanik.

• sequentielle Lösung (Physik (Multiphysik)): verschiedene Modelle werden für mehrere Physiken erstellt, die Lösung einer Physik wird durchgeführt, dann Zustands- oder Ergebnisgrößen an das nächste Modell der anderen Physik übergeben und anschließend die Lösung der nächsten Physik) durchgeführt (uni-direktionale Kopplung von Physiken und Modellen), die Übergabe der Zustands- oder Ergebnisgrößen erfordert ein Mapping (Interpolation), typische Anwendung: CFD-Temperaturfeld-Strukturmechanik, Übertragung von Druck- und Temperatur-Ergebniswerten.

• h-Methode (Diskretisierung): feinere Vernetzung, überwiegend im technischen Alltag der FEM verbreitet, Vorteil: höhere Genauigkeit, Nachteil: neue Diskretisierung, höherer Rechenaufwand.

• p-Methode (Diskretisierung): höherer Ansatzfunktionsgrad, geegnet für Prinzip- und vereinfachte Anwendungen der FEM, Vorteil: höhere Genauigkeit, Nachteil: höherer Rechenaufwand.

• Submodelltechnik (Diskretisierung): sequentielle Simulation mit einer groben Vernetzung und danach einem weiteren Modell mit feinerer Vernetzung eines Details des Bauteils, überwiegend im technischen Alltag der FEM verbreitet, Vorteil: höhere Genauigkeit, Nachteil: neue Diskretisierung, höherer Rechenaufwand durch mehrere Simulationsschritte.

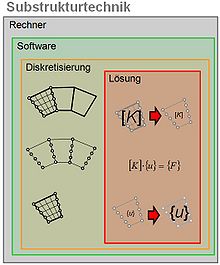
• Substrukturtechnik (Modellbildung): (siehe Prinzip-Skizze rechts) Modellierung, Modellbildung, der Anwender kann vor der Diskretisierung Bauteilbereiche abtrennen und die Lösung aufteilen.

• Direkte Lösung: Lösung des Gesamtgleichungssystems durch Berechnung der Inversen der [K]-Matrix. Für diese Methode muss Arbeitsspeicher (RAM) und Plattenplatz verfügbar sein.

• Iterative Lösung: Lösung des Gesamtgleichungssystems durch iterative Näherung der Freiheitsgrad-(DOF)-Lösung. Für diese Methode muss der Prozessor schnell sein.

• ALE (Diskretisierung): (arbitrary Lagrange Eulerian, siehe auch wikipedia:Arbitrary_Lagrangian_Eulerian) Modellierung mit teilweise Euler-Diskretisierung (raumfeste Vernetzung), teilweise Lagrange-Diskretisierung (Material-feste Vernetzung), wird vom Anwender bei der Idealisierung (Modellbildung) und Diskretisierung berücksichtigt, erfordert eine geeignete Kopplung der beiden Teile der Simulation, typische Anwendung: FSI (Fluid-Struktur-Kopplung), Airbag-Simulation (CFD-Strukturmechanik).

• Unterraum-Methode (Lösung: Algorithmen): (subspace) Algorithmus zur Berechnung von Eigenwerten, betrifft damit Beulen und die Modalanalyse der Strukturdynamik, setzt eine entsprechende Programmierung in der Simulations-Software voraus.

• Matrix-Dekomposition oder domain decomposition (Lösung: Algorithmen): Algorithmus zur parallelen Lösung eines Gleichungssystems, siehe auch wikipedia: Matrix decomposition oder auch en.wikipedia: Domain decomposition methods, setzt eine entsprechende Programmierung in der Simulations-Software voraus. Dabei wird das Modell in Gruppen von Elementen (domains) zerlegt und die Lösung gruppenweise ausgeführt. Dabei kann auch diese numerische Arbeit auf verschiedene Prozessoren oder Rechner verteilt werden, so dass mit der parallelen Abarbeitung ein Zeitgewinn (speed-up) erreicht wird. Der Anwender sollte bei der Nutzung dieser Methode beachten, dass die einzelnen Elementgruppen (domains) unabhängig voneinander sein sollten, so dass die Lösung ohne Datenaustausch untereinander stattfinden kann. Zum Beispiel sollten Kontakt- und Target-Elemente so arrangiert werden, dass sie jeweils nur innerhalb einer Elementgruppe (domain) liegen.

• Gebiets-Zerlegung (Lösung: Algorithmen): (domain decomposition) Algorithmus zur parallelen Lösung eines Gleichungssystems, dabei wird das Modell geometrisch in Bereiche zerteilt und jeweils einem Rechner/Prozessor zur Lösung zugeteilt, setzt eine entsprechende Programmierung in der Simulations-Software voraus.

• Multigrid-Verfahren (Lösung: Algorithmen): Algorithmus zur schnellen Lösung eines Gleichungssystems, betrifft iterative Lösung, setzt eine entsprechende Programmierung in der Simulations-Software voraus.

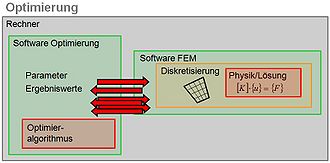
• Optimierung (Lösung: Algorithmen): (siehe Prinzip-Skizze rechts) Kopplung von Optimier-Software und Analyse-Software, typischerweise ist die Optimier-Software übergeordnet und ruft die Analyse-Software auf mit Vorgabe von Eingangs-Parametern, wartet und erhält Ergebnis-Werte zurück.

• Co-Simulation (Lösung: Algorithmen): (co-operative simulation) gleichzeitiger paralleler Ablauf von verschiedenen Programmen und fortgesetzter Datenaustausch zwischen den Programmen, setzt eine geeignete Steuerung oder Synchronisierung voraus.

• Kopplung von Software (Lösung: Algorithmen): typische Anwendung: Software zur Berechnung von Wellenlasten gekoppelt an eine FEM-Software zur Simulation der Strukturmechanik einer Offshore-Windkraftanlage.

• Steuerung der Lösung (Lösung: Steuerung, Zeitschritte): mit der Vorgabe und Steuerung der Konvergenzgrenzen und Zeitschrittweiten kann der Anwender die iterative Lösung lenken.

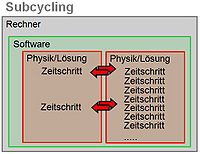
• Subcycling, Substepping (Lösung: Steuerung, Zeitschritte): damit kann bei Multiphysik-Anwendungen die Zeitschrittweite jeder Physik für sich gesteuert werden, erfordert ein Synchronisieren der einzelnen Physiken. Wenn zum Beispiel ein Temperaturfeld mit einem Aufheiz-Abkühl-Zyklus simuliert wird (der in Minuten oder Sekunden abläuft) und eine mechanische Schwingung (bei der es um Millisekunden geht), sollte nicht die gekoppelte Lösung mit einer Zeitschrittweite von Millisekunden (das wäre zu ineffektiv) oder von Sekunden (das wäre für die mechanische Schwingung zu ungenau) gerechnet werden. Am besten wäre ein Lösungsablauf, bei dem 1000 Schritte der mechanischen Schwingung berechnet werden und erst dann ein Schritt des Temperaturfeldes "mitgenommen" wird.

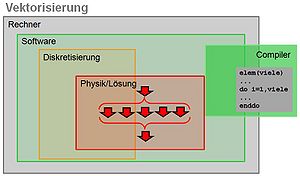
• Vektorisierung (Hardware): (siehe Prinzip-Skizze rechts) programm-interne Vorbereitung für Vektor-Abarbeitung, setzt Compiler-Möglichkeiten und teilweise Programmier-Eingriffe voraus, veraltet (früher war Vektorisierung bei Großrechner-Prozessoren vorbereitet), im Ergebnis vergleichbar zu Parallelisierung (Unterschied anhand eines Beispiels von geschachtelten Schleifen im Programm: für Vektorisierung sollte die längste Schleife innen liegen, für Parallelisierung sollte die längste Schleife außen liegen).

• SMP, DMP, MPP, DDS (Hardware, Middleware): (shared memory parallel, distributed memory parallel, message passing process, wikipedia:DDS )Hardware Architektur, kann zur schnellen Lösung beitragen, setzt im allgemeinen keinen Anwender-Aufwand voraus, aber entsprechend ausgestattete Software, die Verwaltung und Abstimmung der Arbeiten der Prozessoren erfordert zusätzliche Rechenzeit.

• GPU (Hardware): (wikipedia:Graphics Processing Unit), Prozessor für die Grafik. Kann bei entsprechender Software-Auslegung einbezogen werden in das "number crunching" bei der Lösung.

• SaaS, Cloud (Hardware): (wikipedia:Software as a Service, Outsourcing), Auslagerung der rechenintensiven Lösung auf Rechner eines externen Anbieters. Dies kann vorteilhaft sein, um Lastspitzen und kurzfristigen Bedarf zu decken. Zu bedenken sind Geheimhaltung der Daten, Verfügbarkeit, Zugriffs-Prioritäten, Ausfallsicherheit, Exportvorschriften.

Anmerkungen

• nichtlineares Verhalten - insbesondere Kontakt - verringert den Nutzen von allen Methoden zur Parallelisierung der Lösung.
• Alle Methoden zur Parallelisierung der Lösung hängen direkt mit der vorhandenen Hardware zusammen.
• Bei einer Simulation mit Parallel-Processing kann im praktischen Alltag nie genau die Aufteilung auf die Kerne und die Belegung der Speicherbereiche festgelegt werden. Dadurch können durchaus die Ergebnis-Zahlenwerte beeinflusst werden (Beispiel: Zeitverlauf-Simulation_Kontakt_Genauigkeit).

Fallbeispiele

Publikationen hierzu finden Sie unter Hardware Fallbeispiele.

Weiterführende Informationen

Ein Info-Webinar speziell hierzu finden Sie bei
ANSYS HPC-Solvertechnologie