Antwortspektrumanalyse Theorie
Aus ESOCAETWIKIPLUS
engl: response spectrum method Kategorie: Level 3 Theorie Mechanik
Allgemeine Informationen hierzu finden Sie zum Beispiel bei wikipedia:Antwortspektrum
Hier werden Grundlagen zur Antwortspektrumanalyse in der Strukturdynamik dargestellt.
Grundlagen
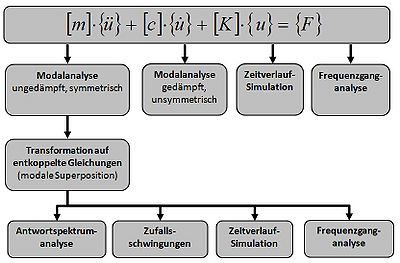
Die Antwortspektrum-Methode baut auf der Modalanalyse auf. Ebenso wie bei der modalen Superpositionsmethode wird das Gleichungssystem entkoppelt. Die Transformation in ein entkoppeltes System geschieht durch einen Produktansatz für die Verschiebungsgrößen, wobei die Ortsabhängigkeit durch die Eigenvektoren Φi und die Zeitabhängigkeit durch die noch unbekannte Funktionen yi(t) beschrieben wird (Gl. 1)
Da höhere Eigenformen meist unbedeutend sind, wird näherungsweise ein reduzierter Ansatz mit nur p (p < n) Eigenformen verwendet (Gl. 2)
In Matrizenschreibweise ist dies zu schreiben als (Gl. 3)
Setzt man diese Beziehung in die oben genannte Gl. 1 ein und multipliziert man das Gleichungssystem auf beiden Seiten mit ΦT, so ergibt sich (Gl. 4)
Wie bei der modalen Superposition nachgewiesen wurde, haben die Massenmatrix und die Steifigkeitsmatrix in Gl. 44 nur auf der Hauptdiagonalen Werte ungleich Null. Bei Annahme einer modalen Dämpfung oder der Rayleigh-Dämpfung, bei der sich die Dämpfungsmatrix aus Massen- und Steifigkeitsanteilen zusammensetzt, ist auch die Dämpfungsmatrix nur auf der Diagonalen besetzt. Das Gleichungssystem Gl. 4 ist damit entkoppelt und kann geschrieben werden als (Gl. 5)
Jede Zeile i kann also für sich alleine betrachtet werden (Gl. 6)
Wird Gl. 6 mit mi dividiert und werden die bekannten Beziehungen (Gl. 7)
eingesetzt, so ergibt sich (Gl. 8)
wobei
Gl. 8 ist die Bewegungsgleichung eines Einmassenschwingers mit der Steifigkeit ωi2, einer Einheitsmasse, einer Dämpferkonstante ξi ωi und einer zeitlich veränderlichen Kraft γi.
Bis zu dieser Stelle ist das Vorgehen identisch zur Methode der modalen Superposition. Die unbekannten Verschiebungen yi(t) könnten jetzt bei gegebener transienter Belastung durch numerische Integration bestimmt werden. Wie oben beschrieben, sind jedoch bei der Antwortspektrum-Methode die Verschiebungsverläufe nicht von Interesse. Vielmehr wird nach einer Näherung für die maximal auftretenden Verschiebungen gesucht. Daher verwendet die Antwortspektrum-Methode ein vereinfachtes Verfahren, bei dem nur die maximalen Verschiebungen yi max ohne deren zeitlichen Verlauf bestimmt werden. Dies geschieht durch den Vergleich der durch Gl. 8 bestimmten Einmassenschwinger mit einem Antwortspektrum.
Ein Antwortspektrum beschreibt die Antwort von Einmassenschwingern unterschiedlicher Eigenfrequenz auf eine gegebene transiente Belastung. Es ist ein Diagramm der maximalen Verschiebungen (oder Geschwindigkeiten oder Beschleunigungen) als Funktion der Eigenfrequenz der Einmassenschwinger.
Ein solches Antwortspektrum ist z.B. bei Standsicherheitsnachweisen von Bauwerken vorgegeben und dient bei einer solchen Berechnung als Belastung. Der exakte transiente Belastungsverlauf ist dem Endanwender häufig unbekannt.
Aus dem Antwortspektrum wird für jede Eigenfrequenz ein Spektralwert Si abgelesen. Dieser beschreibt die maximale Auslenkung eines entsprechenden Einmassenschwingers.
Da in Gl. 8 auf der rechten Seite aber nicht der reale Kraftvektor enthalten ist, sondern eine Kraft γi, die auf die Eigenform transformiert ist, muss der Spektralwert Si ebenfalls transformiert werden.
Daraus erhält man dann die maximale Verschiebung yi max mit (Gl. 9)
Der Wert γi wird als Partizipationsfaktor (participation factor) bezeichnet. Er gibt an, inwieweit die äußere Belastung in die Richtung der Eigenform wirkt. Ein großer Wert von γ bedeutet, dass die entsprechende Eigenform von der Belastung stark angeregt wird, ein sehr kleiner Wert bzw. ein Wert gleich Null bedeutet, dass die Belastung orthogonal zu dieser Eigenform steht und demzufolge diese Eigenfrequenz nicht angeregt wird.
Bei Krafterregung berechnet sich der Partizipationsfaktor zu (Gl. 10)
und bei seismischer Erregung zu (Gl. 11)
wobei {D} der Vektor der seismischen Anregung ist.
Nachdem die maximalen Auslenkungen yi max bestimmt sind, müssen nun die darausfolgenden Verschiebungen des realen Modells bestimmt werden, d.h. es muss eine Summation aller Eigenformen stattfinden. Dies ist allerdings nicht eindeutig möglich, da keine Informationen über das zeitliche Auftreten der Maxima vorliegen.
Ein konservativer Ansatz hierfür wäre (Gl. 12)
Gl. 12 liefert jedoch bei p>>2 immer zu große Werte, da es unwahrscheinlich ist, dass alle Eigenfrequenzen zum gleichen Zeitpunkt ihre maximale Auslenkung erreichen.
Es gibt eine Reihe von Methoden, diese Summation realistischer durchzuführen. Am häufigsten wird die SRSS-Methode (square root sum square) verwendet (Gl. 13)
Andere Summationsverfahren sind zum Beispiel die “closely spaced modes” Methode. Dabei wird eine direkte Summe der Beiträge der ersten Eigenfrequenzen und eine SRSS-Summation der anderen Eigenfrequenzen durchgeführt. Es kann auch ausgewertet werden, wie weit die Eigenfrequenzen voneinander entfernt sind und in Abhängigkeit davon für dicht benachbarte Anteile die direkte Summation, für weiter voneinander entfernte Anteile dagegen die SRSS-Summation durchgeführt werden.
Ein Antwortspektrum ist nicht zu verwechseln mit einem Anregungsspektrum. Das Antwortspektrum ist die Amplitude eines Einmassenschwingers einer gegebenen Frequenz auf die Anregung. Die Bestimmung des Antwortspektrums erfolgt dadurch, dass die transiente Last als Zeitverlauf zugrundegelegt wird und die Antwort eines Einmassenschwingers mit einer Frequenz auf diese Anregung bestimmt wird. Die maximale Amplitude des Schwingers wird für seine Eigenfrequenz festgehalten. Dies wird für eine Anzahl von Einmassenschwingern (Anzahl n) mit unterschiedlichen Eigenfrequenzen durchgeführt. Die Ergebnisse liefern eine Punktmenge in einem Frequenz-Amplituden-Diagramm. Diese Punktmenge wird durch einen Kurvenverlauf verbunden und damit das Antwortspektrum festgelegt.
Weiterführende Informationen
Ein weiterführendes Seminar speziell hierzu finden Sie unter "Wissen" auf der Homepage von CADFEM.